A. Sagheer and Crossroads
暴力
需要注意:只要该路口有人,则不能有车。
代码如下:
#include <cstdio>
#include <iostream>
#include <vector>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
int q[5];
int c[5];
int x[5];
int main(void){
int l,s,r,p;
scanf("%d%d%d%d",&l,&s,&r,&p);
if(l)c[4]=1;
if(s)c[3]=1;
if(r)c[2]=1;
if(p)q[1]=1;
if(l+s+r)x[1]=1;
scanf("%d%d%d%d",&l,&s,&r,&p);
if(l)c[1]=1;
if(s)c[4]=1;
if(r)c[3]=1;
if(p)q[2]=1;
if(l+s+r)x[2]=1;
scanf("%d%d%d%d",&l,&s,&r,&p);
if(l)c[2]=1;
if(s)c[1]=1;
if(r)c[4]=1;
if(p)q[3]=1;
if(l+s+r)x[3]=1;
scanf("%d%d%d%d",&l,&s,&r,&p);
if(l)c[3]=1;
if(s)c[2]=1;
if(r)c[1]=1;
if(p)q[4]=1;
if(l+s+r)x[4]=1;
bool f=0;
for(int i=1;i<=4;++i)
if((c[i]==1&&1==q[i])||(q[i]==1&&x[i]==1))f=1;
if(f)printf("YES\n");
else printf("NO\n");
}B. Sagheer, the Hausmeister
题目大意:给定一个楼层的亮灯状态,问从左下角开始灭掉所有灯最少需要走几步。不需要回到起点。
dp
记录最高需要到达的层数$fl$ ,每层楼最左边亮着的灯$l[i]$ 以及最右边亮着的灯$r[i]$ .
定义状态$dp[i][0]$ 表示灭完第$i$ 层灯后在左边楼梯所需要的最少步数,$dp[i][1]$ 表示灭完第$i$ 层灯后在右边楼梯所需要的最少步数。复杂度$O(nm)$.
需要注意:$fl=0$ 时,需要特判。
代码如下:
#include <cstdio>
#include <iostream>
#include <vector>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
typedef long long ll;
int inf=100000000;
int n,m,l[20],r[20],dp[20][2],fl=-1;
char str[20][105];
int main(void){
scanf("%d%d",&n,&m);
for(int i=n-1;i>=0;--i)
scanf("%s",str[i]);
for(int i=0;i<n;++i){
for(int j=0;j<m+2;++j)if(str[i][j]=='1'){
if(l[i]==0)l[i]=r[i]=j;
else r[i]=j;
fl=i;
}
}
if(fl==-1){
printf("0\n");
return 0;
}
dp[0][0]=2*r[0],dp[0][1]=m+1;
for(int i=1;i<n-1&&i<fl;++i){
dp[i][0]=min(dp[i-1][0]+2*r[i],dp[i-1][1]+m+1)+1;
dp[i][1]=min(dp[i-1][0]+m+1,dp[i-1][1]+2*((l[i]!=0)?(m+1-l[i]):0))+1;
}
if(fl!=0)printf("%d\n",min(dp[fl-1][0]+r[fl],dp[fl-1][1]+((l[fl]!=0)?(m+1-l[fl]):0))+1);
else printf("%d\n",r[0]);
}枚举
注意到该题$n \leqslant 15$ ,故可以用$2^{15}$ 枚举灭完各层灯后所在的楼梯状态,复杂度为$O(nm+n \times 2^n)$.
代码如下from xdujlx:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
int l[20],r[20];
char s[105];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=n;i>=1;i--){
scanf("%s",s);
for(int j=1;j<=m;j++)
if(s[j]=='1') r[i]=j;
for(int j=m;j>=1;j--)
if(s[j]=='1') l[i]=j;
}
for(;n>=2&&!l[n];--n);
int ans=1e9;
if(n==0) ans=0;
else for(int i=0;i<(1<<(n-1));i++){
bool pL=1;
int res=n-1;
for(int j=1;j<n;j++){
bool L=(i>>(j-1))&1;
if(pL!=L){
res+=m+1;
pL=L;
}
else if(pL&&r[j]) res+=2*r[j];
else if(!pL&&l[j]) res+=2*(m+1-l[j]);
}
if(pL&&r[n]) res+=r[n];
else if(!pL&&l[n]) res+=(m+1-l[n]);
ans=min(ans,res);
}
cout << ans << endl;
return 0;
}C. Sagheer and Nubian Market
题目大意:有$n$ 个物品,每个价值$a_i$ 。若购买$k$ 个物品(这些物品下标为$x_1,x_2,…x_k$),则每个物品需要支付$a_{x_i}+kx_i$元 。现有$s$ 元,问最多能买多少个物品。
二分
二分$k$ 值,每次用优先队列检查是否能在$s$ 元内购买$k$ 个物品,复杂度为$O(nlog_2^2(n))$.
代码如下:
#include <cstdio>
#include <iostream>
#include <vector>
#include <map>
#include <set>
#include <algorithm>
#include <queue>
using namespace std;
typedef long long ll;
ll n,s,a[100005],sum;
priority_queue<ll>q;
void init(ll x){
while(!q.empty())q.pop();
for(int i=1;i<=n;++i)q.push(-(a[i]+x*i));
}
bool check(ll x){
init(x);
sum=0;
for(int i=0;i<x;++i){
sum+=-q.top();
q.pop();
if(sum>s)break;
}
return sum<=s;
}
int main(void){
scanf("%I64d%I64d",&n,&s);
for(int i=1;i<=n;++i)
scanf("%I64d",&a[i]);
ll l=0,r=n;ll mid=(l+r)>>1;
while(l<=r){
if(check(mid))l=mid+1;
else r=mid-1;
mid=(l+r)>>1;
}
if(check(r))printf("%I64d %I64d\n",r,sum);
else printf("0 0\n");
}D. Sagheer and Kindergarten
题目有毒,暂时放弃治疗。
E. Sagheer and Apple Tree
题目大意:给定一颗$n(n \leqslant 10^5)$ 的树,且每个结点上都有$a_i$ 个苹果,每次操作只能将一个结点上的若干个苹果(不能为空)移到它的孩子结点或者将一个孩子结点上的若干个苹果(不能为空)吃掉。现在两人轮流进行操作,后手先将两个不同结点的苹果个数互换后,先手开始操作,直到不能操作为输。问有多少种换苹果的方案,使得先手输。
博弈
考虑一条链的情况
当结点数为1时
该结点上没有苹果时,如下所示:

显然此时$SG$ 值为$0$ 。
该结点上有$n$ 个苹果时,如下所示:
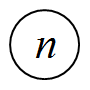
由于其能转移到$0 \sim n-1$ 的任意状态,故此时$SG$ 值为$n$ 。
当结点数为2时
父节点有$n$ 个苹果,孩子上无苹果时,如下图所示:
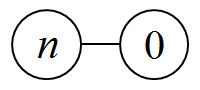
考虑先手无论从父节点移多少苹果到孩子,后手都将其吃掉,故先手必败,$SG$ 值为$0$ 。
当结点数为3时
父节点有$n$ 个苹果,孩子和孙子结点上无苹果时,如下图所示:
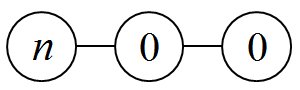
若将$n$ 个苹果全部移到孩子结点,则转移到了上面两个结点的状态($SG=0$),故若设该状态$SG=f(n)$ ,那么$f(n) \geqslant 1$ 。
将$n-m$ 个苹果移到孩子结点,如图:
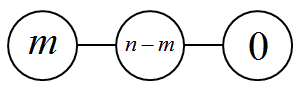
设该状态$SG=f(m)$ ,而该状态其实是由
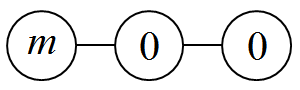
和
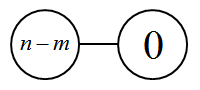
组合而成的,设前半部分的$SG$ 值为$f(m^{‘})$ ,后半部分的$SG$ 值为$0$ ,故有$f(m)=f(m^{‘}) \oplus 0=f(m^{‘})$ ,其中$\oplus$ 表示异或操作。
有了上面的结论后,有$f(n)$ 可以转移到$f(m)$ ,故$f(n)=n$ 。
当结点数为更多时
父节点有$n$ 个苹果,后继结点上均无苹果时,不难得到:
- 当结点数为奇数时,$SG=n$ ;
- 当结点数为偶数时,$SG=0$ 。
总结
单条链的$SG$ 值为所有奇数结点的苹果个数的异或和。
考虑一颗树的情况
一颗树其实是由若干条链组合而成的,因为题目中说明所有叶节点的深度同奇偶,故一棵树的$SG$ 值为与叶节点同奇偶的所有结点上苹果个数的异或和。
换苹果的方案
设初状态的$SG$ 值为$res$ ,所有层数与叶节点奇偶性相同的结点组成的集合为$S$ ,所有层数与叶节点奇偶性不同的结点组成的集合为$T$。
若$res=0$ ,即没交换前先手已经为输,此时$S$ 中结点可以互相交换,$T$ 中结点也可以互相交换。
之后将$T$ 中每个结点与$res$ 异或得到$temp_x$,若在$S$ 中找到与$temp_x$ 相等的结点,那么这两个结点可以互相交换。
代码如下:
#include <cstdio>
#include <vector>
#include <map>
#define X first
#define Y second
#define N 100005
using namespace std;
int n,a[N],p;
long long ans;
vector<int>e[N],b[2];
map<int,int>mp[2];
int dfs(int u,int d){
int deep=d;
b[d&1].push_back(a[u]);
mp[d&1][a[u]]++;
for(int i=0;i<(int)e[u].size();++i)
deep=max(deep,dfs(e[u][i],d+1));
return deep;
}
int main(void){
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
for(int i=2;i<=n;++i){
scanf("%d",&p);
e[p].push_back(i);
}
int d=dfs(1,0);
int res=0;
for(int i=0;i<(int)b[d&1].size();++i)
res^=b[d&1][i];
if(res==0){
int tot=b[d&1].size();
ans+=(long long)tot*(tot-1)/2;
tot=b[!(d&1)].size();
ans+=(long long)tot*(tot-1)/2;
}
for(map<int,int>::iterator it=mp[!(d&1)].begin();it!=mp[!(d&1)].end();++it){
int temp=res^it->X;
ans+=(long long)(it->Y)*mp[d&1][temp];
}
printf("%I64d\n",ans);
}